Neural Optimal Transport for Dynamical Systems

Methods and Applications in Biomedicine

I defended my PhD! Neural optimal transport for biomedicine? A overview below with the thesis highlights.

But first, a huge thank you to my advisors Andreas Krause and Marco Cuturi, my committee Lucas Pelkmans and Jure Leskovec, and all collaborators for such an incredible adventure!

The full thesis is available for download here.

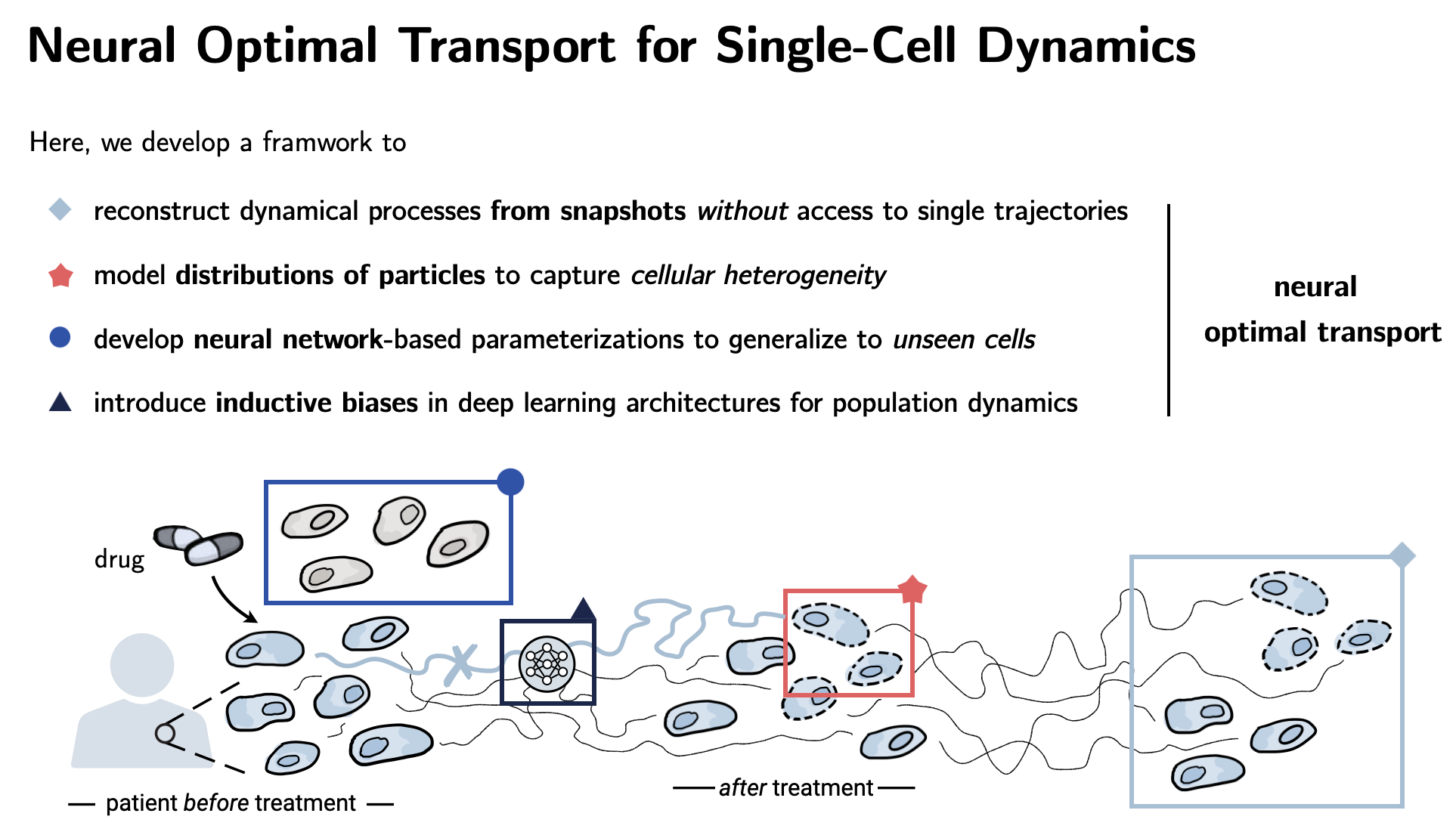	This thesis develops machine learning methods for modeling dynamical systems. Central application: drug discovery and single-cell biology with the aim to predict single cell responses to perturbations such as drugs. Challenge: We cannot trace the response of individual cells.
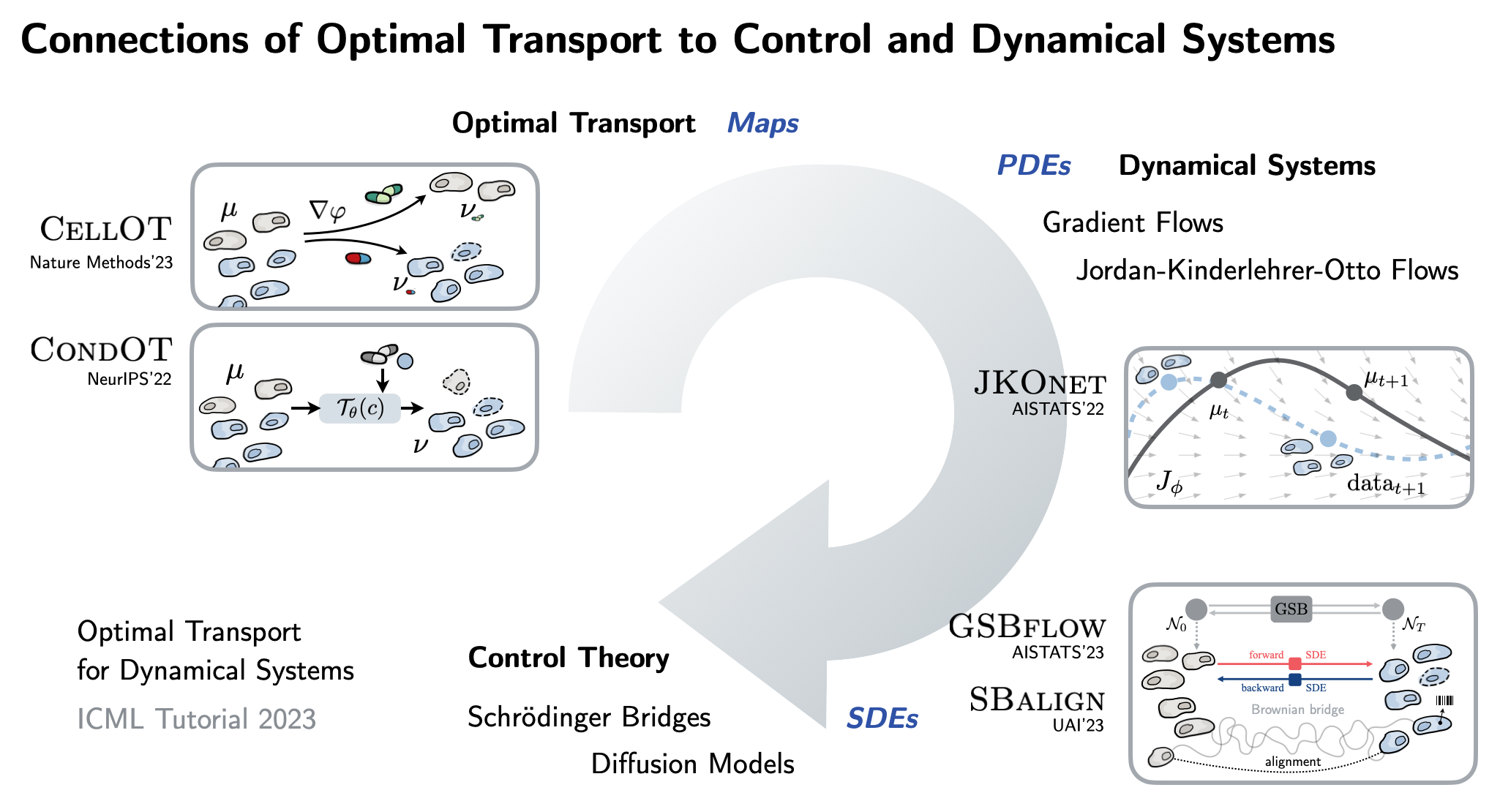	To achieve this, this thesis connects a variety of seemingly unrelated concepts into a unified framework: We propose #neural optimal transport methods that can be parameterized through static maps or dynamic ODEs, SDEs, PDEs. See also our ICML 2023 tutorial for a deep dive!
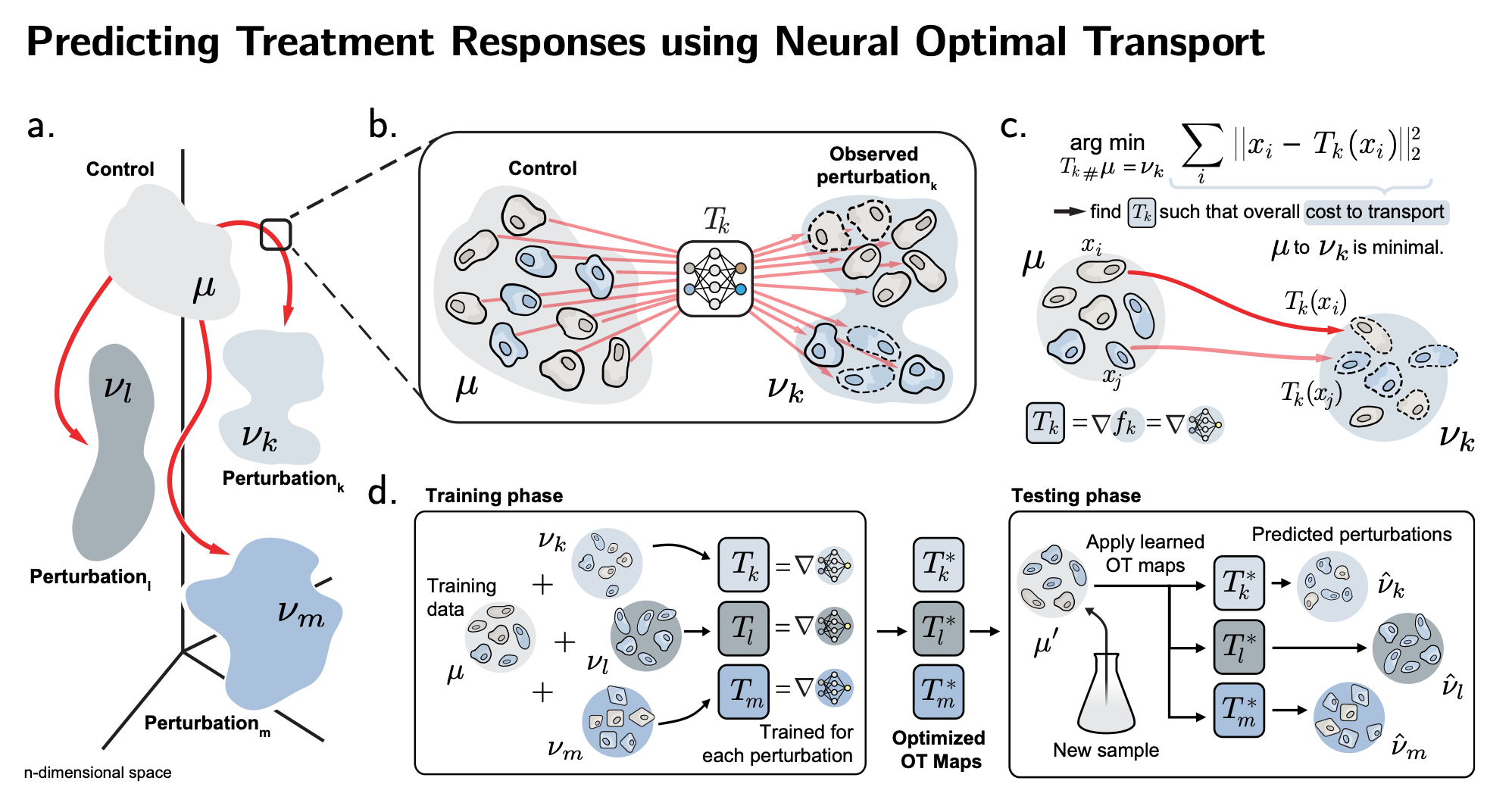	The first method, CellOT (Nature Methods'23) uses optimal transport to accurately predict single-cell responses to various drugs or developmental signals. We learn a neural Monge map that transforms the unperturbed cell population into its perturbed state. Have a look at our Research Briefing in Nature Methods and the feature in ETH Press
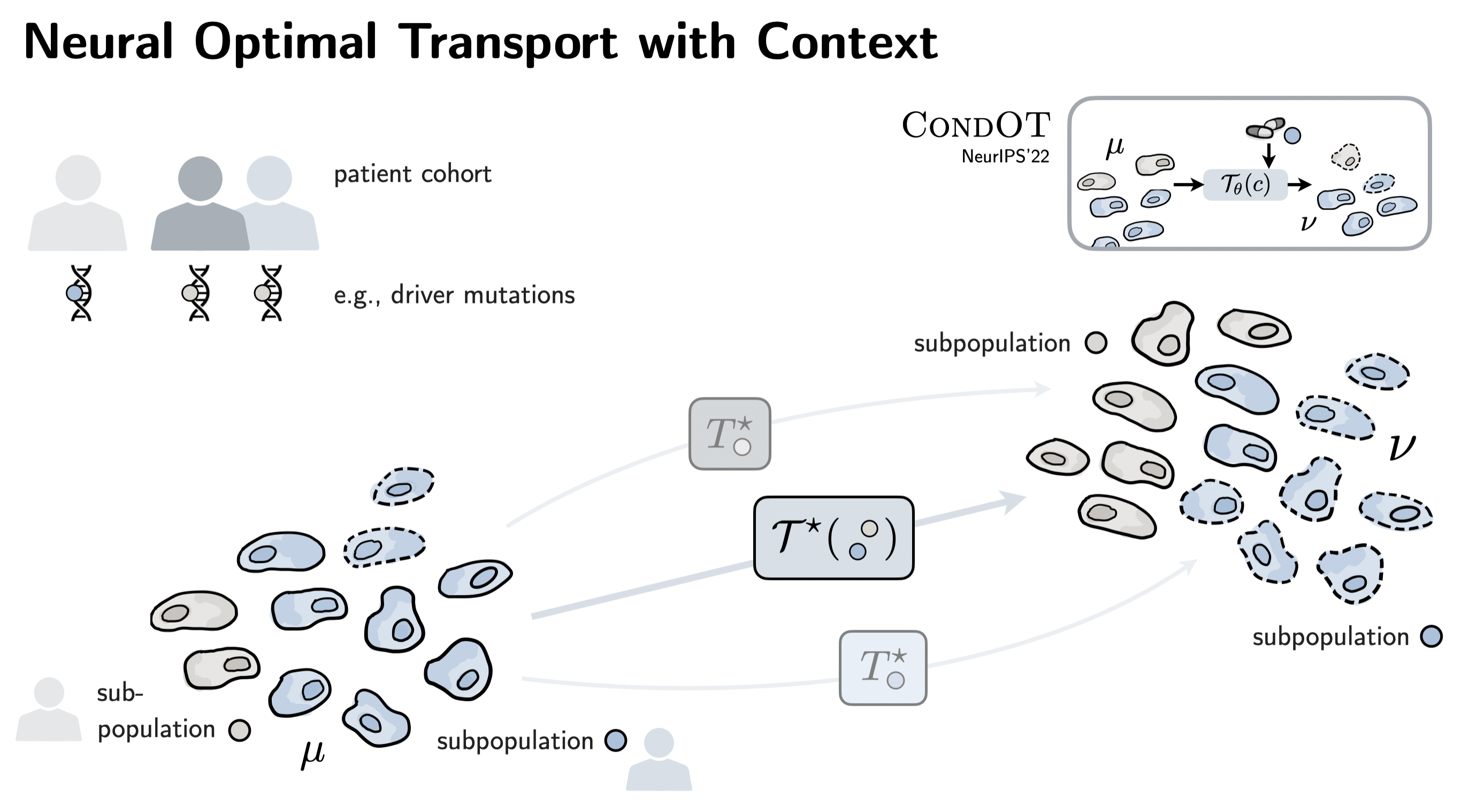	CondOT (NeurIPS'22) generalizes CellOT and allows conditioning the inferred responses on a context, e.g., patient meta-information. This is crucial when moving to prediction tasks on patient cohorts!
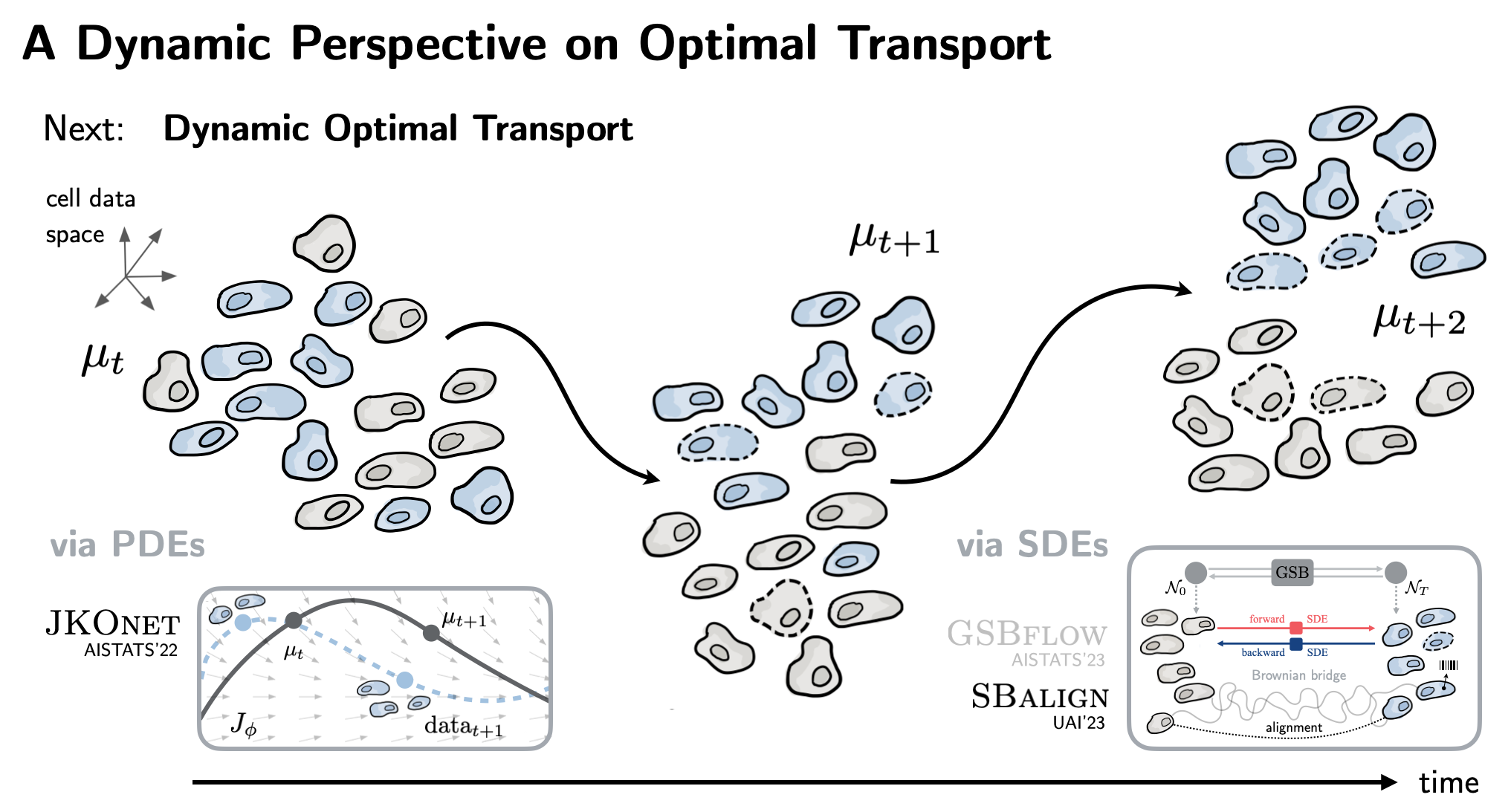	Moving beyond such static formulations, we explore OT's connections to dynamical systems theory. The result is JKOnet (AISTATS'22) that learns the underlying epigenetic landscape in order to predict how cells differentiate into various lineages.
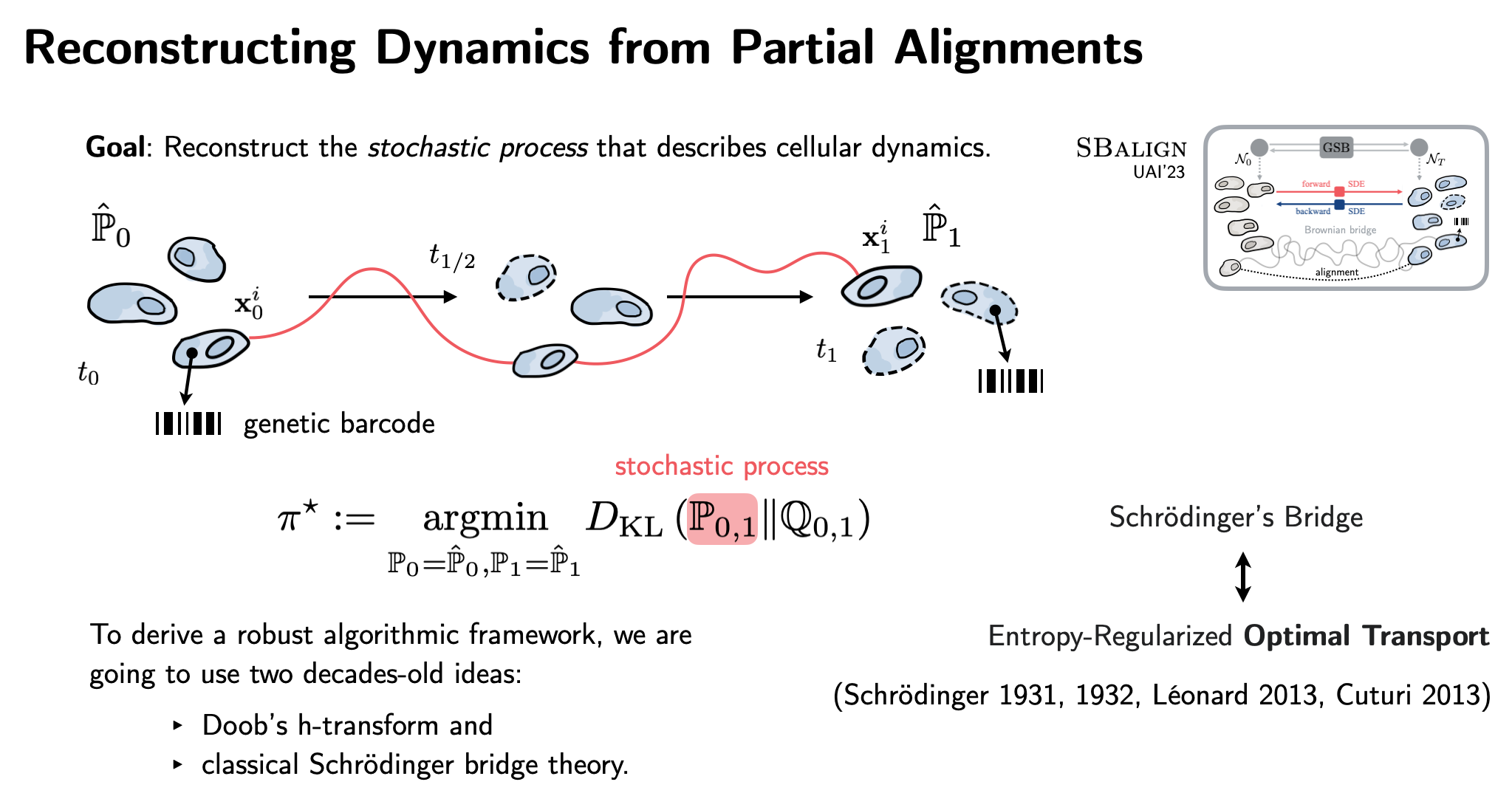	Lastly, building on SDE theory, diffusion models, and flow matching, SBalign (UAI'23) combines OT with powerful score-matching architectures. Taking advantage of biotech innovations such as DNA barcoding, we infer continuous single-cell dynamics from snapshots!